数学作为其他很多学科的基础学科,很多学科都在借鉴数学中的思维方式,而欧氏几何提出的公理化思维更是被很多人推崇备至,从这门学科中提取思维模型的精华,除了在生活中简单的计算是对数学的应用,在思考和决策中,对数学的应用将极大的提升我们的决策质量。
这篇文章中,我将重点介绍生活中常见的几种数学思维模型,希望对你有所帮助
1、排列与组合
排列组合使我们了解我们周围世界的实际概率,事物是如何排序的,以及我们应该如何思考这些事。
2. 代数等价
代数的引入可以使我们用数学和抽象方法证明两个看似不同的事物很可能是相同的。通过数学符号的表现,我们可以证明等价性和非等价性,使用这个方法使人类具备了无限的工程和技术能力。至少知道代数基础,就能让我们理解各种重要的结果。
3. 随机性
尽管人类大脑很难理解,但世界的大部分都是由随机的、非连续的、无序的事件构成的。当我们事物的因果关系归因到我们控制之外的事情上,我们就会被“随机”影响愚弄。
若我们不去纠正这种随机影响的愚弄——我们就会产生一种错误的意识——即倾向于认为事情更容易被预测,并据此开始行动。
1913年,在蒙特卡罗赌场。当轮盘赌连续26次落在黑色区域的时候,一群赌徒因此损失了数百万美元。当时在场的人一致认为,下次会落在红区。
每次落在黑色区的时候,他们就认为落在红色的区的可能性更高。我们将这种错误称为蒙特卡罗谬误(或者赌徒谬误)——假设先前的结果会影响未来的结果。
而实际上,未来的结果也是独立的。换句话说:人们是在假设一个随机的过程变得不那么随机,而且随着不断被重复而更容易被预测。
阿莫斯·特沃斯基和丹尼尔·卡尼曼认为这种思维方式是“典型性试探法”的组成部分,他们指出我们越是相信我们可以控制随机事件,我就越可能被赌徒谬误所击垮。
4.随机过程
(泊松、马尔科夫和随机漫步)随机过程是一个随机的数据统计过程,它涵盖了各种各样的过程,其中单个变量的变化是无法被预测,但可以通过概率来思考。
各种随机方法可以帮助我们通过概率描述变量系统,而不一定要确定当个变量在某一时间上的位置。
举个例子,我们不可能每日都预测出股票的价格,但我们可以描述出它们随时间变化的各种分布概率。很明显,股市(随机过程)更可能在一天之内上涨或下跌1个百分点,而不可能是10个百分点,尽管我们无法预测明天会是什么样的。
生活的最大特点是不确定性,随机现象无处不在、无时不在,大起大落常发生在须臾之间,但我们天生趋向于忽视低概率事件的可能性。随机事件发生的可能性用概率衡量。
5. 复利思维
据说爱因斯坦说复利为世界第八大奇迹。虽然他可能并未说过此话,但复利确实堪称一项伟大的奇迹。
复利是一个变化的过程,每次产生的利息都和本金和此前的利息加在一起,然后产生新的利息,实现无限增值(俗称利滚利,和单利相比,复利中的利息也可以产生利息)。
这会产生一种指数增长,而非简单的线性增长或递加增长。复利是一个非常重要,非常底层的模型,马太效应、临界点效应、边际成本递减等等思维模型都可以从这个模型推导。
金钱并非复利效应会发生作用的唯一领域,思想想法和情感关系也是一样。在有形领域,复利增长会受到物理条件的限制,从而导致回报递减;而在无形领域,复利增长更为自由。复利还导致了货币的时间价值,这也是现代金融的基础。
复利原理要表达的意思是:
1、复利周期内看似不起眼的小进步或者小退步,假以时日,则会让本体产生超乎想象的巨大进步或者退步。
2、做事耐心点,把时间当做朋友。
3、不要高估你一年能做成的事,也不要低估你五年能做成的事。
6. 乘以“0”(归零)
任何一个受过教育的人都知道,任何数,不管数值多大,只要乘以“0”,结果仍然是0.这个道理不管是在人类系统还是数学领域都是正确的。在某些系统中,在某一领域的一次失败,就能抵消在所有其他领域中创造的成功。
就像这个简单的乘法运算表示的那样,修正零点通常要比扩大其他领域的效用大的多。
7. 归纳与统计
统计学揭示了很多现实规律,例如全世界人口的身高、智商遵循正态分布,财富分布遵循二八法则,世界上80%的科学定律和技术革新是由20%的人完成的,互联网产品市场占有率遵循赢家通吃,人们学习英语、锻炼身体的曲线是一条先陡升在平缓的对数曲线,而企业的成长、个人财富的增长更多的是符合先平缓再陡升的指数曲线。
当我们理解了这些行为背后的运行规律时,我们就更能科学地看待我们所处的环境和状态,用更平和的心态面对眼前的问题和瓶颈。
统计让我们认识行为背后真实规律的同时,也让我们放弃了很多不现实的幻想。我们都知道今天的大数据和人工智能其实就是建立在统计学的概念上,只是传统的统计学样本是有限的,而大数据是全部数据,我们通过统计分析寻找事物背后的规律。
8. 大数定律
在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。通俗地说,这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。偶然中包含着某种必然。大数定律分为弱大数定律和强大数定律。
与大数定律相反的是小数定律,小数定律提醒我们应该谨慎看待通过小型样本所得出的结论。(小数定律会让我们滥用典型,形成管窥之见)
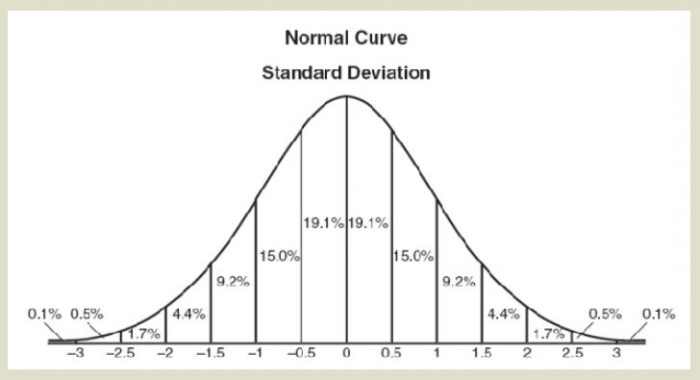
9. 钟形曲线/正态分布
正态分布是一个数据统计过程,可以用著名的钟形曲线进行图形表示。在正确的抽样统计中,会出现一个有实际意义的平均值和越来越小的标准差(因此也被称为中心极限定理)。
比较著名的例子包括人的身高体重的分布,但需要注意的是,在非有形的系统中,比如人类的社会系统,并不遵循正态分布定律。
10. 幂次定律
最常见的不满足正态分布的过程是“幂次定律”,即一个数量变量随着另一个变量呈指数关系,而非线性关系。例如里氏震级描述了地震在幂律分布范围内的威力:8级地震比7级的破坏力大10倍,9级比8级的威力大10倍。
中心极限理论无法应用于地震的描述中,因为在地震中并不存在平均值一说。所有的幂律分布都是这样。
11、均值回归
在概率领域,有这么一个概念,叫做「均值回归」。均值回归:指股票价格、房产价格等社会现象、自然现象(气温、降水),无论高于或低于价值中枢(或均值)都会以很高的概率向价值中枢回归的趋势。
根据这个理论,一种上涨或者下跌的趋势不管其延续的时间多长都不能永远持续下去,最终均值回归的规律一定会出现:涨得太多了,就会向平均值移动下跌;跌得太多了,就会向平均值移动上升;
12、贝叶斯定理
贝叶斯定理,在机器学习满天飞的时代,简直可以被成为做简单的机器学习模型了。定理本身一目了然:P(A|B) = P(B|A) * P(A)/P(B)用语言解释就是:在B出现的前提下,A出现的概率等于A和B都出现的概率除以B出现的概率。换句话说就是后验概率和先验概率的关系。
示例:就是事件A 在另外一个事件 B 已经发生条件下的发生概率.条件概率表示为 P(A|B),读作“在 B 条件下 A 的概率”.
事实上,我们可以用贝叶斯定理来搭建一个思考的框架,不断的动态调整我们的看法或态度,在经过一系列的事情证实后,就会形成比较稳定而正确的看法。
大多数人对事物的看法是摇摆不定的,因为我们的直觉思维是粗放而快速,所以很难稳定下来。
而运用贝叶斯定理以后,它能够量化我们的看法,不致于因个人的偏好而偏差太远,而且哪怕你给定的先验概率是随便写的,也没关系,经过几次事实的印证后,它会越来越接近于真相。

愿你在探索智慧的路上走得更远~




















